在写今天关于减法器文章之前,我需要多解释一下,计算机那点事儿xxx这一系列内容实际是我在读《编码-隐匿在计算机软硬件背后的语言》这本书时做的验证,目的是在加深自我理解的同时,能够成体系的梳理一下对计算机软硬件的认识,因此,一些方法和概念更偏向于直接告诉大家结果,而不是根据认知去推理这些方法的由来,就像上一篇计算机那点事儿之加法计算器中,针对用逻辑门来标识1bit加法器的进位和加和位这种方法,我也是根据书中的介绍进行展开。所以,在很多衔接部分就比较生硬,当然我也没有打算要在这个阶段去补上这些环节,可能会在很久很久以后,或者是我被隔离了实在有时间,会将自己知道的这些内容,完整的表述出来,而目前能做的,就是先让这些内容呈现出来而已。
在计算机那点事儿之加法计算器中,我们介绍了如何通过基本的逻辑电路搭建一个8Bit的加法器。本篇我们来介绍如何来通过改造上一篇中的加法器,实现一个不完整的减法器。之所以是不完整的,是我们没有在这里讨论结果是负数的情况(即减数大于被减数)。
问题
实现一个减法器(被减数大于减数)
思考
在加法计数器中,我们解决的是进位问题,在减法中,我们比较关注的是借位问题。
这一次,我们需要先明确我们目前掌握的工具,与门、或门、非门、与非门、或非门、异或门以及8bit加法器。
因此,我们不必像加法器中那样分析结果,我们用另一种方式来观察一下两个十进制数241和135的减法: $$ \begin{array}{r} 241-135=106 \end{array} $$ 在这里,我们在个位减法中,需要向十位借1,至今我仍然觉得,这是小学算术中很抽象的一个动作,十位要是不借呢?为了防止十位不借(减少这一步操作,去凑一个用电路更方便实现的做法),我们需要对借位这个动作做一些改造,我们将这个算式改写成这样: $$ 241+(999-135)+1-1000=106 $$ 为了避免借位发生,我们在计算时,给等式左边先加了999+1,再减1。用数学老师的话来说,我们对等式做了一次恒等变形。
我们解释一下这个999-135,这个动作叫做对减数取十进制的补数。135对9取补数,135的补数是864。通过这动作,我们就可以避免借位操作,而且在二进制中,这个动作做起来异常容易。
取补完成后,我们将被减数与减数的补数相加,结果+1,再减去1000,即可得到最终的结果。
分析
根据如上思考过程,我们可以将十进制的减法避免借位的这种方法,推广到二进制中。
这里,需要补充一下,二进制求补码的操作:
在二进制中(对1的补数),只需将原来的二进制数的1变为0,0变为1即可。因此,对1求补数有时也称为相反数(negation),或反码(inverse)。
举个例子,求135的补数:
135 10000111
inreverse 01111000
方案
这里再强调一下,我们针对的是减数小于被减数的减法。因为负数在二进制的标识是另一个概念,二进制中只有0和1,关于符号位的表示,我们在这一篇不做讨论。接下来,我们总结一下我们的方案:
- 减数求对1的补数:直接使用反向器进行取反;
- 被减数+减数:借助上一节的加法器;
- +1:对上一节加法器进行改造,将第0位的进位输出改连接到加/减法选择位(原来是直接接0)。即,选择减法时,我们该位为1,即实现+1操作;
- 减去一个
1 0000 0000,因为我们这减数和被减数都是8位:我们用一个CO输出位来表示减法的状态:- 加法时,和以前一样,这一步表示一个加法和的最高位;
- 减法时,
- 当该位为1时,表示当前减法得到了一个负数(下溢,underflow);
- 当该位位0时,则当前减数是小于被减数;
实验过程
按照上述方案,我们对加法器进行了如下改造:
- 增加1个加法、减法切换按钮,这里用SUB来代替;
- 0表示加法
- 1表示减法
- 最低位的进位位输入改为接到SUB按钮,即当为减法时,该为位1,用来执行+1操作;
- 最高位(原第9位)的输出,该为输出与SUB按钮求异或(XOR),来输出,代表的含义如上。
接下来,我们来用我们的减法器来计算:241-135
241 11110001
135 10000111
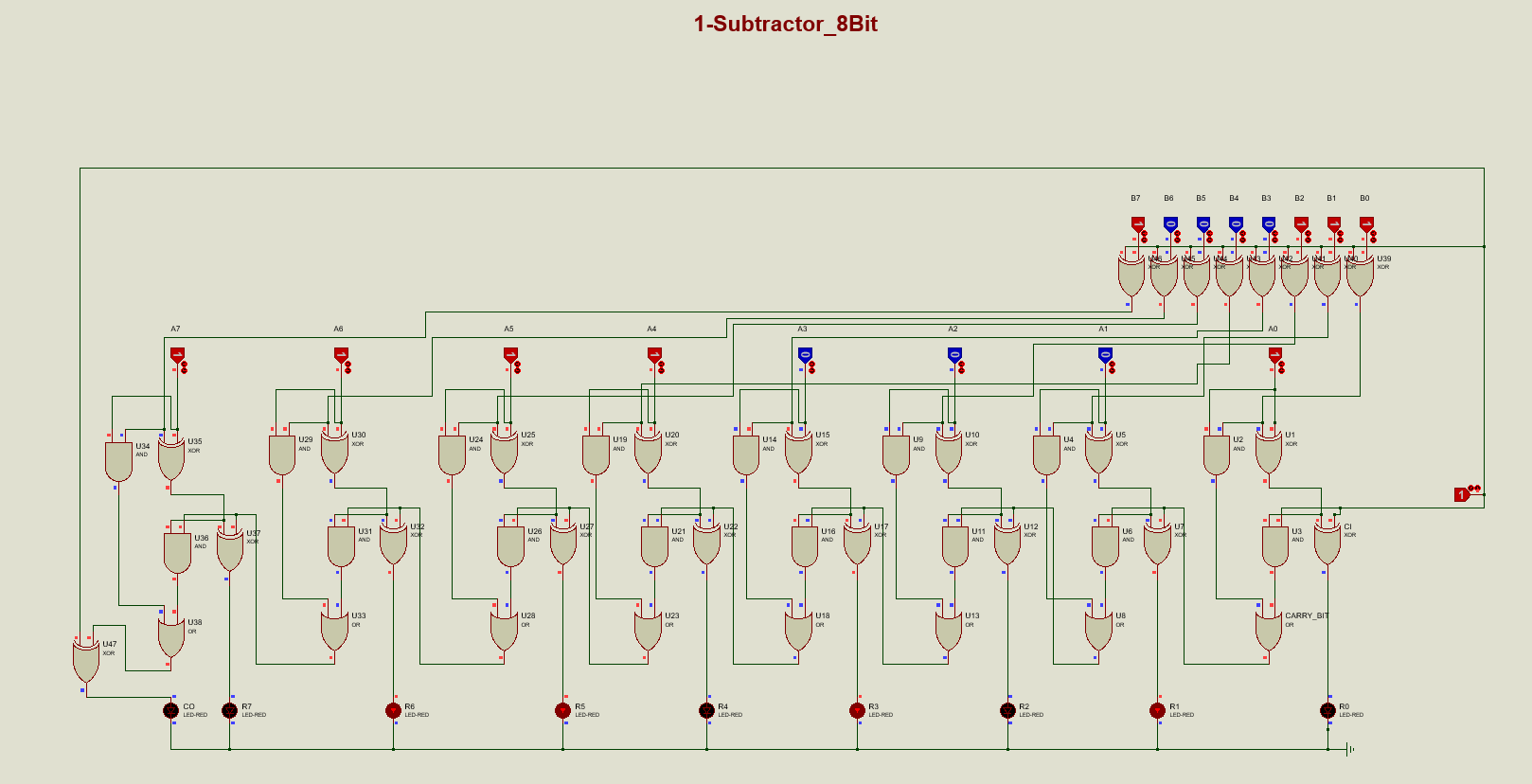
图中的结果显示为:溢出位为0,结果为0110 1010,即十进制表示为106;
至此,我们就可以完成了这个简易的减法器。
结论
- 我们通过对加法器进行改造,增加了1个异或门、8个取反器、1个加/减法切换开关,实现了基本的减法器。